طريقة حساب مساحة الدائرة

• ذات صلة
• قانون شبه المنحرف
• كيفية حساب محيط المثلث

الدائرة

عندما تسمع بكلمة "دائرة" فيتبادر إلى ذهنكَ بأنّها عبارة عن شكل دائري دون زوايا أو حواف، وفي الهندسة يمكن تعريف الدائرة بأنها شكل مغلق ثنائي الأبعاد منحني الشكل،ففي حياتنا الكثير من الأشكال الدائرية مثل إطارات السيارات وساعة الحائط وغيرها، ويعد مركز الدائرة هو نقطة المركز فيها والتي تبعد عنها جميع النقاط في الدائرة بنفس المسافة، وتسمى المسافة بين أي نقطة في الدائرة وبين نقطة المركز نصف قطر الدائرة، ويسمى الخط المستقيم الذي يمرّ بمركز الدائرة ويصل بين أي نقطتين في الدائرة بقطر الدائرة، وتسمى جميع النقاط المحيطة بمركز الدائرة بمحيط الدائرة، ويسمى الخط الذي يمرّ بجانب الدائرة ويمسها في نقطة واحدة (المماس)، ويسمى الخط الذي يمس الدائرة عند قطتين (قاطع)، ويسمى الخط الذي يصل بين أيّ نقطتين على محيط الدائرة دون المرور بمركز الدائرة (وتر)، ويسمى أيّ جزء من محيط الدائرة (قوس).^[١][٢]

طريقة حساب مساحة الدائرة

مساحة الدائرة هي المنطقة المحصورة داخل محيط الدائرة، وإذا أردت حساب مساحة شكل دائري احسب مساحة الدائرة إذا كان لديك طول نصف القطر من خلال هذا القانون (مساحة الدائرة = نق²× π)، إذ أن (نق) هو نصف قطر الدائرة، و(π) هو قيمة ثابتة لا تتغير وتساوي (3.14)، وإذا كان لديك محيط الدائرة وتريد حساب مساحتها، فيمكنك حسابه من خلال القانون (مساحة الدائرة = محيط الدائرة ² /(4×π))، وللتوضيح أكثر سنعطي بعض الأمثلة:^[٣]

• احسب مساحة الدائرة إذا علمت أن نصف قطرها يساوي 6 سنتمتر؟ من خلال القانون يمكننا حلها (المساحة = نق²× π)، المساحة =36×3.14 = 113.04 سنتمتر مربع.
• احسب مساحة الدائرة إذا علمت أن قطرها يساوي 20 إنش؟ (القطر = 2 × نق) ومنه فإن مساحة الدائرة = ((ق/2)² × π) ومنه فإن مساحة الدائرة = 100×3.14 = 314 إنش تربيع.
• احسب مساحة الدائرة إذا علمت أن محيطها يساوي 42 سنتمتر؟ يمكن حساب مساحة دائرة من خلال القانون مساحة الدائرة = محيط الدائرة ² /(4×π)، ومنه فأن مساحة الدائرة = 42 ² / (4×3.14) = 140.4 سنتمتر مربع.

طريقة حساب محيط الدائرة

كما ذكرنا سابقًا فإن محيط الدائرة هو طول جميع النقاط التي تبعد نفس المسافة عن نقطة المركز، وقد تحتاج في حياتك لحساب محيط دائرة ما؛ مثل حساب طول سياج تريد وضعه حول حوض استحمام، أو مجرد أنك تريد حلّ مسألة رياضية، لذا فإن عليك معرفة كيفية حساب محيط الدائرة، ويمكنك حسابه إذا كان طول قطرها معلوم من خلال القانون (محيط الدائرة = قطر الدائرة × π)، وكما قلنا فإن قيمة π تساوي 3.14، وإذا كان نصف القطر معلوم فيصبح القانون (محيط الدائرة= 2 × نصف القطر × π)، وللتوضيح أكثر فإننا سنعطيك بعض الأمثلة:^[٤]

• احسب محيط الدائرة إذا علمت أن قطرها يساوي 5 سنتمتر؟
  • يمكن حساب محيط الدائرة من خلال القانون (محيط الدائرة = قطر الدائرة × π)، وبالتالي فإن المحيط = 5×3.14=15.7 سنتمتر.
• احسب محيط الدائرة إذا علمت أن نصف قطرها يساوي 5 إنش ؟
  • يمكن حساب محيط الدائرة من خلال القانون (محيط الدائرة= 2 × نصف القطر × π)، وبالتالي فإن محيط الدائرة = 2×5×3.14 = 31.4 إنش.

المساحة

ما هي المساحة؟ وكيف تحسب؟ لا بد أنك قد تعاملت في حياتك مع الكثير من الأشكال الهندسية واحتجت لحساب مساحة شكل ما سواء أكان منتظم الشكل أو غير منتظم، ولفهم ما تعنيه المساحة في الرياضيات يُمكن القول بأنّ المساحة هي مصطلح يستخدم لتحديد مقدار الفراغ الذي يشغل شكل معين أو سطح ثنائي الأبعاد، وتقاس المساحة بوحدات مربعة مثل السنتمتر المربع والمتر المربع، وكلّ شكل من الأشكال الهندسية له قانون لحساب مساحته، وسنذكر فيما يلي بعض الأمثلة على الأشكال الهندسية والقوانين التي تحسب بها مساحتها:^[٥][٦]

• الدائرة : تحسب مساحة الشكل الدائري من خلال قانون (المساحة = نق ² × π)، إذ نق هي نصف القطر، و(π) هي قيمة ثابتة تساوي 3.14.
• المربع : تحسب مساحة المربع من خلال القانون (المساحة = طول الضلع ² ).
• المثلث: تحسب مساحة المثلث من خلال قانون (المساحة =0.5 × طول القاعدة × الارتفاع).
• المستطيل: تحسب مساحة المستطيل من خلال القانون (المساحة = الطول × العرض).
• متوازي الأضلاع: تحسب مساحة متوازي الأضلاع من خلال القانون (المساحة = طول القاعدة × الارتفاع).
• البيضوي : تحسب مساحة الشكل البيضوي من خلال القانون (المساحة = نصف القطر القصير× نصف القطر الطويل × π).
• شبه المنحرف: تحسب مساحة الشكل شبه المنحرف من خلال القانون (المساحة = 0.5 × (القاعدة الأولى + القاعدة الثانية) × الارتفاع).

قد يُهِمُّكَ

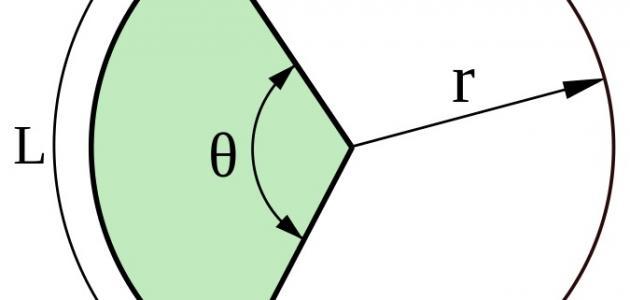
عرفت مما سبق كيف تحسب مساحة الدائرة، ولكن قد تحتاج في حياتك إلى حساب مساحة جزء من الدائرة فقط، وبما أن قياس زوايا الدائرة كاملة تساوي 360 درجة، فإن نسبة زاوية القطع الدائري تتناسب مع 360 درجة، وتتناسب مساحة القطع الدائري مع مساحة الدائرة كاملة، وتوجد علاقة طردية بين كلّ من مساحة القطع الدائري وطول قوس القطع مع زاوية القطع الدائري، فكلما زادت زاوية القطع زادت مساحة القطع الدائري وزاد طول القوس، وكلما قلت الزاوية قلت مساحة القطع الدائري وقل طول القوس، ولحساب مساحة القطع الدائري يمكنك استخدام أحد القوانين التالية:^[٧][٨]

• القانون الأول : إذا كنت تعرف مساحة الدائرة كاملة وزاوية القطع فإن (مساحة القطاع الدائري = مساحة الدائرة كاملة × π(زاوية القطع/360)، وبما أن (مساحة الدائرة كاملة = نصف القطر ² ×π)، يصبح القانون كاملًا (مساحة القطاع الدائري= نق²π××(ز/360))، حيث (نق) هو نصف القطر، و(ز) هي زاوية القطع.
• القانون الثاني : إذا كنت تعرف طول قوس القطع الدائري، فإن (مساحة القطع الدائري =((نصف القطر×طول القوس)/2) .

ولتوضيح الطريقة أكثر سوف نذكر لك بعض الأمثلة:

• احسب مساحة القطع الدائري إذا كان نصف القطر يساوي 5 سنتمتر، وكانت زاوية القطع الدائري تساوي 60 درجة؟
  • في هذه الحالة نستخدم القانون (مساحة القطع الدائري=نق ² × π×(ز/360)) = 25×3.14×(60/360) =13.09 سنتمتر مربع.
• احسب زاوية القطع الدائري إذا كانت مساحة القطع الدائري تساوي 35.4 سنتمتر مربع، وكان نصف القطر يساوي 6 سنتمتر؟
  • في هذه الحالة نستخدم قانون (مساحة القطع الدائري=نق ² × π×(ز/360))، ومنه فإن زاوية القطع= 112.67 درجة.

المراجع

1. ↑ "Circle", mathsisfun, Retrieved 2020-6-23. Edited.
2. ↑ "What is a Circle? ", splashlearn, Retrieved 2020-6-23. Edited.
3. ↑ "How to Calculate the Area of a Circle", wikihow, Retrieved 2020-6-23. Edited.
4. ↑ "How to Calculate the Circumference of a Circle", wikihow, Retrieved 2020-6-23. Edited.
5. ↑ "What is area?", theschoolrun, Retrieved 2020-6-23. Edited.
6. ↑ "Area of Plane Shapes", mathsisfun, Retrieved 2020-6-23. Edited.
7. ↑ "Sector area", mathopenref, Retrieved 2020-6-23. Edited.
8. ↑ "Area Of A Sector and Segment", onlinemathlearning, Retrieved 2020-6-23. Edited.