محتويات
كم عدد أضلاع الدائرة؟
لا تمتلك الدائرة أيّ ضلع، فالضلع خط مستقيم، والخط المستقيم هو أقصر مسافة بين نقطتين، وباعتبار أنّه لا يمكن أن تكون أيّ نقطتين على الدائرة على نفس الخط المستقيم فإنّ عدد أضلاع الدائرة هو صفر.[١][٢]
قد تتساءل الآن ماذا تُسمّى حدود الدائرة إذا لم تكن ضلعاً؟ إنّها تُسمى المحيط، حيث يتكوّن شكل الدائرة الهندسي من عدد لا نهائي من النقاط التي لا تقع على نفس الخط المستقيم، وإنّما تقع على نفس المستوى وعلى نفس المسافة من نقطة ثابتة تُسمّى المركز، فيتشكّل بذلك محيطها، [١] ومجموعة النقاط التي تُحيط بها الدائرة تُشكّل شكل القرص الدائري والذي يكون إمّا مفتوحًا أو مغلقًا.[٣]
تعرّف على خصائص الدائرة
ندرجُ لك في ما يأتي أهم الخصائص المُتعلّقة بالدائرة:[٤]
- تنقسم الدوائر إلى نوعين؛ دوائر متطابقة لها نفس أنصاف الأقطار، ودوائر متشابهة لها أنصاف أقطار مختلفة.
- يُعتبر قطر الدائرة هو أطول وتر في الدائرة.
- تقابل الأقواس المتساوية زوايا مركزية متساوية، والعكس صحيح، وكذلك تُقابل الأوتار المتساوية لدائرة ما زوايا مركزية متساوية، ولتتوضّح لكَ الصورة أكثر، افترض أنّكَ أخذت قطاع دائري وأخذت مُقابله بالضبط قطاع دائري آخر، فعندها ستكون الزوايا المتقابلة متساوية، وكذلك الأقواس المتقابلة متساوية، وإذا قمتَ بالتوصيل بين نقطتي طرفي القوس سيتشكل لديك وتر يساوي في طوله طول الوتر المقابل له.
- يُنصّف الوتر بواسطة أنصاف الأقطار المتعامدة عليه.
- يُمكن أن تحيط الدائرة بمستطيل، أو شبه منحرف، أو مثلث، أو مربع، وفي حال مسّت رؤوس أو حواف هذه المُضلعات نقاطاً على الدائرة سيتشكّل ما يُسمّى بالمماس، والذي يُمكن أيضاً تشكيله برسم دائرة داخل هذه المضلّعات بحيث تكون أضلاع المضلّعات ماسّة لمحيط الدائرة.
- إذا رُسم مماس في نهايتي القطر، فإنّ المماسين الناتجين يكونان متوازيان مع بعضها البعض.
- يتشكّل مثلث متساوي الساقين من نصفيّ قطر الدائرة، والوتر الواصل بين طرفيهما.
بعض الصيغ الرياضية المتعلقة بالدائرة
لكل شكل هندسي صيغ رياضية خاصة لحساب محيطه ومساحته، وفيما يأتي سنعرفك بالصيغ والقوانين التي تخص الدائرة:[٤]
- قطر الدائرة = 2× نصف قطر الدائرة.
- محيط الدائرة= 2×π×(نصف القطر)
- مساحة الدائرة = π×(نصف القطر)²
ماهي أجزاء الدائرة؟
للدائرة مجموعة من الأجزاء سنعرفك عليها لتكون قادراً حساب العمليات الرياضية الخاصة بالدائرة:[٥]
- الوتر: هو أيّ قطعة مستقيمة تصل بين نقطتين على محيط الدائرة.
- القطر: هو أيّ قطعة مستقيمة تصل بين نقطتين على الدائرة بشرط مرورها بمركز الدائرة، بالتالي يُمكنكَ اعتبار أنّ كلّ قطر هو وتر وليس العكس.
- نصف القطر: هو القطعة المستقيمة الواصلة بين مركز الدائرة وأيّ نقطة على محيطها.
- المماس: هو خط يمر بنقطة واحدة فقط على الدائرة.
- القاطع: هو خط لا نهائي على امتداد وتر الدائرة، ويقطع الدائرة في نقطتين فقط.
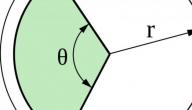
- القوس: هو جزء من محيط الدائرة، ويُمكن حساب طوله من خلال العلاقة: a = θ⋅r، حيث θ هي الزاوية بالتقدير الدائري بين نصفي قطر الدائرة، و r هو نصف قطر الدائرة.
- القطاع الدائري: هو جزء من الدائرة يحدّه نصفا قطر وقوس، ولتتوضح لكَ الصورة أكثر، تخيّل أنّك تمتلك بيتزا وأخذت لنفسك قطعة منها، ماذا تُسمّى هذه القطعة؟ نعم إنّها قطاع دائري.
- القطعة الدائرية: القطعة الدائرية هي جزء من الدائرة يفصلها عن بقية الدائرة مستقيم قاطع أو وتر، ويُمكن تعريفها على أنّها المساحة بين الوتر وقوس الدائرة دون المرور بمركز الدائرة.
سؤال وجواب
هل الدائرة مضلّع؟
لا، الدائرة منحنى وليست مضلّع.[٦]
كم عدد زوايا الدائرة؟
مجموع قياس زوايا الدائرة = 360 درجة، لكن من المهم أن تعرف أنّ الدائرة ليست مضلعاً ليكون لها زوايا ثابتة، ولا يُمكن أن تتواجد الزوايا ما لم تتواجد الأوتار، والقواطع، في هذه الحالة يختلف عدد زوايا الدائرة على حسب كلّ مسألة.[٧]
كم قطر للدائرة؟
تمتلك الدائرة عدد لا نهائي من الأقطار، فكل وتر في الدائرة يمر بالمركز يُعتبر قطراً.[٨]
كم عدد الرؤوس في الدائرة؟
لا يوجد رؤوس للدائرة، فالرأس هو نقطة التقاء ضلعين، وباعتبار أنّ عدد الأضلاع التي تمتلكها الدائرة يساوي صفراً فإنّ عدد الرؤوس في الدائرة يساوي صفراً أيضاً.[٩]
المراجع
- ^ أ ب "How many sides does a circle have?", Quora, 27/12/2019, Retrieved 27/6/2021. Edited.
- ↑ "Circles and using a Compass", Maths Teacher, Retrieved 27/6/2021. Edited.
- ↑ "Disk", Mathworld, Retrieved 19/8/2021. Edited.
- ^ أ ب "Properties of Circle", BYJU's, Retrieved 27/6/2021. Edited.
- ↑ "Circle Properties", Maple Soft, Retrieved 27/6/2021. Edited.
- ↑ "Questions and answers - polygons", Vendantu, Retrieved 19/8/2021. Edited.
- ↑ "How many angles does a circle have?", Quora, Retrieved 19/8/2021. Edited.
- ↑ Miriam Snare, "How to Find the Diameter of a Circle: Definition, Formula & Example", Study. Com. Edited.
- ↑ "How Many Vertices Does a Circle Have?", Reference , 29/3/2020, Retrieved 19/8/2021. Edited.